Le problème du pharaon

 

Des archéologues ont découvert qu’un Pharaon avait décidé d’ériger une stèle en forme de parallélépipède rectangle pour fêter sa dernière victoire. Cette stèle devait être construite avec des pierres cubiques de 10 cm de côté et avoir une hauteur égale à la diagonale de sa base. Ces cubes devaient préalablement être entreposés dans un nombre premier de dépôts. Toutefois les archéologues n’ont retrouvé qu’un seul dépôt. Ce dernier contenait exactement 348960150 pierres.

Les archéologues ont alors réussi à déterminer qu’une seule stèle était possible. Laquelle ?

 

solution

 

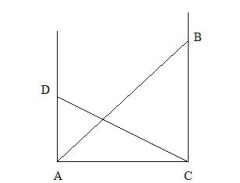
La largeur du couloir



Une échelle AB de longueur 3 mètres est posée en travers d’un couloir, de manière à ce que l’extrémité A soit dans l’angle d’un couloir. Une deuxième échelle CD, de longueur 2 mètres est également posée de travers dans ce couloir, l’extrémité C étant dans l’angle opposé à A. Les deux échelles se croisent à un mètre du sol et on demande la largeur AC du couloir, au centimètre près. 

solution

Ecrivons :

2^2 = 2 + 2

3^2 = 3 + 3 +3

4^2 = 4 + 4 + 4 +4

et plus généralement  x^2 = x + x + ... + x (x fois)

Dérivons la dernière ligne : 2x = 1 + 1 + ... +1 (x fois) = x, soit 2x = x

Où est l'erreur ?

 

Si vraiment vous ne trouvez pas, regardez l'explication

Considérons l’équation : x2 + x + 1 = 0 et raisonnons :

 

x2 + x + 1 = 0  =>  x3 + x2 + x = 0 (on a multiplié par x)

                        =>  x3 + x2 + x + 1 = 1 (on ajoute 1)

                        =>  x3 = 1 (rappelons que x2 + x + 1 = 0 au départ)

                        =>  x = 1

 

Mais à partir de x2 + x + 1 = 0 on ne peut pas logiquement obtenir

x = 1

Où est la faute ?

 

Cherchez bien avant de regarder l'explication

 
 

retour à la page des problèmes