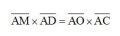Ces sujets sont des exercices de mathématiques, donnés en classe de troisième, dans les années 1960 et 1961 (source : Monge et Guinchan)

Racine carrée :

Pour former un parterre carré, on plante 324 oignons de tulipe en rangées parallèles distantes les unes des autres de 12 cm. Dans chaque rangée, les oignons sont eux-mêmes distants les uns des autres de 12 cm ; il y a un oignon à chaque sommet du carré.

1° Calculer le côté de ce parterre.

2° Autour de ce parterre, et à 12 cm de chacun des côtés, on sème une bande de gazon de 50 cm de large. Calculer l'aire  de la pelouse de gazon.

Proportionalité (on disait aussi rapports) :

Un oncle avait primitivement partagé sa fortune entre ses trois neveux proportionnellement aux nombres 7, 6 et 5. Mais il se ravise et refait le partage proportionnellement aux nombres 6, 5 et 4. L'un des neveux reçoit ainsi 1200 F de plus qu'auparavant. Quelle est la valeur de l'héritage et quelles sont les parts des trois neveux ?

Algèbre :

Soit l'expression algébrique : 

(1)     E = (7x + 1)(4x + 1) - (14x + 2)(5x - 3) + 49x² - 1

1° La développer, la réduire et l'ordonner par rapport aux puissances décroissantes de x. On appellera (2) la forme ainsi obtenue de l'expression de E.

2° Reprenant la forme (1) de l'expression E, la transformer en un produit de facteurs du premier degré. On obtiendra ainsi la forme (3) de l'expressionde E.

3° Calculer les valeurs numériques de E pour x = 0 ; x = -1/3 ; x = -1/7  x = -4

On choisira, pour chaque cas, la forme de l'expression E qui permet le calcul le plus rapide.

Equation du premier degré à une inconnue :

Soit l'expression :

y = (4x² - 1)² - (2x + 1)²

1° La développer et l'ordonner par rapport aux puissances décroissantes de x.

2° La transformer en un produit de facteurs du premier degré.

3° Calculer la valeur numérique de y pour  x = √2 -1

4° Calculer les valeurs de x pour lesquelles on a : y = 0

Systèmes d'équations du premier degré :

1° Calculer les nombres m et p de façon que le polynôme :

y = mx³ + px² - 9x + 18

prenne la valeur zéro dans les deux cas suivants : 

a) quand on remplace x par 2

b) quand on remplace x par -3

2° Après avoir remplacé m et p par leur valeur, mettre le polynôme obtenu sous la forme d'un produit de trois facteurs.

Applications de la fonction linéaire :

Un jeune homme se propose de remonter un fleuve en canot à vapeur dont la vitesse est 18 km/h en eau calme. La vitesse du courant est 3 km/h. Le jeune homme quitte l'embarcadère A à 14 heures.

1° A quelle heure doit-il faire demi-tour s'il veut être de retour en A 4 heures plus tard ?

2° Quelle est la distance qui sépare de A le point extrême B qu'il aura atteint ?

3° Représenter graphiquement, en fonction de la durée écoulée depuis l'heure du départ, la distance y du canot à l'embarcadère (1 cm représente 20 min sur Ox ; 1 cm, 2,5 km sur Oy).

4° Calculer les heures auxquelles le canot se trouve à 25 km de A.

Equation du second degré à une inconnue (ce chapitre n'est plus au programme du collège) :

Une pipette cylindrique de 20 cm de long est plongée à moitié dans du mercure ; on la ferme à la partie supérieure et on la soulève hors du mercure. Une partie du mercure s'écoule. Quelles seront alors les longueuers occupées par l'air et le mercure , Hauteur barométrique 76 cm.

Quinze persones, hommes et femmes, ont dîné dans un restaurant. La dépense totale a été de 108 F. Bien que chaque femme ait dépensé 3 F de moins que chaque homme, la dépense totale pour les femmes a été la même que la dépense totale pour les hommes. Trouver le nombre d'hommes, de femmes et le prix des repas.

Théorème de Thalès :

Soit un trapèze ABCD, de bases AB et CD, I le point de rencontre des diagonales. Les parallèles menées par I aux cotés AD et BC coupent respectivement la base AB en A' et B'.

Montrer que : AA' = BB'.

Triangles semblables :

On considère deux cercles de centres O et O', de rayon R et R' (R > R'), tangents extérieurement en T. Soient A et A' les points de contact de ces cercles avec une de leurs tangentes communes extérieures, S le point d'intersection des droites OO' et AA'.

1° Montrer que les points S et T divisent le segment OO' dans le même rapport k. Calculer k en fonction de R et R'.

2° Soient B et B' les points où la droite OO' recoupe les cercles (O) et (O'). Comparer les rapports SA/SA', SB/ST et ST/SB'. En déduire la valeur du rapport SB/SB', en fonction de R et R'.

Triangles et théorème de Pythagore :

1° trouver le rapport des cotés du triangle équilatéral inscrit et du triangle équilatéral circonscrit à un même cercle.

2° Même question pour l'hexagone régulier.

Notions de trigonométrie : 

Un observateur est placé à 8 m au-dessus du plan horizontal qui passe par le pied d'un édifice ; il voit le sommet de celui-ci sous un angle de 23° au-dessus de l'horizontale et le pied sous un angle de 9° au-dessous de l'horizontale.

1° A quelle distance de cet édifice se trouve l'observateur ?

2° Quelle est la hauteur de l'édifice ?

Relations métriques dans le cercle :

Dans le triangle ABC les angles en A et en C sont tels que l'angle en A est égal à deux fois l'angle en C. Soit I le pied sur BC de la bissectrice intérieure de l'angle en A.

1° Comparer les triangles ABC et ABI. En déduire la relation :

BA² = BI . BC                  (1)

Montrer que le cercle circonscrit au triangle AIC est tangent en A à AB.

2° Le cercle circonscrit au triangle AIB recoupe en D la droite AC. Montrer que : BA = BD

3° Comparer les triangles BCD et AIC. En déduire la relation : 

AB . AC = CB . CI            (2)

4° En utilisant les relations (1) et (2) montrer que : 

AB . AC = BC² - AB²

Mesure des aires :

Soient un cerc le de centre O et de diamèter AB = 2R et, sur le prolongementde AB au-delà de B, un point C tel que BC = 4R. Sur le une droite variable passant par A et coupant de nouveau le cercle O en D, on prend un point M tel que :

1° Etudier les deux triangles ADO et AMC.

2° Quelle particularité le quadrilatère ODMC présente-t-il ?

3° La droite AD tourne autour du point A. Sur quelle ligne le point M se déplce-t-il ?

4° Soit α (alpha) la mesure de l'angle (OAD). Pour quelle valeur de α les droites OD et CM sont-elles parallèles ?

5° Pour quelle valeur de α ces droites sont-elles perpendiculaires ?

Calculer dans ce cas, en fonction de R, l'aire du quadrilatère ODMC.

Géométrie dans l'espace :

Soit ABC un triangle, tel que AB = AC = 10 cm ; BC = 12 cm. En A, on élève une perpendiculaire au plan ABC, et on considère un point mobile D sur cette perpendiculaire.

1° Montrer que la droite qui joint le point D au milieu M du segment BC est toujours perpendiculaire à BC.

2° Si AD = 8 cm, quelle est la nature du triangle ADM ? En déduire la valeur de l'angle (AMD). Calculer AD pour que l'angle (AMD) = 60°.

Volumes :

On trouve chez les libraires des presse-papiers en cristal qui ont été obtenus ainsi : on enlève à chaque sommet d'un cube une pyramide. La base de cette pyramide est un triangle dont les sommets sont les milieux de trois arêtes du cube.

1° Combien un tel presse-papier a-t-il de sommets, de faces ? Que sont ces faces ?

2° La longueur d'une arête du solide est a. Evaluer son aire totale.

3° Quel serait le volume du cube primitif ?

4° Déterminer le volume et l'aire latérale d'une des pyramides telles que SABC

5° Calculer le volume de ce presse-papier.

Application numérique : a = 5 cm.