Actualité

carrés magiques

Deux manières d'écrire un nombre : calculons 1/3. Nous obtenons 0,333333.... c'est à dire le chiffre 0 suivi d'une infinité de décimales. Calculons maintenant 3 x 1/3 : nous obtenons 0,99999999..... Mais si nous calculons 1/3 + 1/3 +1/3 nous obtenons 3/3 c'est à dire 1.

La conclusion s'impose : 0 suivi d'une infinité de fois la décimale 9 (soit 0,99999...) est égal à 1.

Le plus grand nombre premier connu est 2^43112609 - 1, c'est-à-dire un nombre de 12.978.189 chiffres. Pour donner une idée, si nous écrivons ce nombre à une taille raisonnable (10 chiffres pour 4 cm), il faudrait prévoir une feuille de papier de presque 52 kilomètres de long et un peu plus de 4 mois de travail (en écrivant jour et nuit, sans s'arrêter)

Mise à jour de février 2013 : le plus grand nombre premier connu est désormais 2^57885161-1 et ce nombre a plus de 17 millions de chiffres

L'injustice des élections.

Supposons trois candidats, Pierre, Jacques et Louis que nous notons P, J et L pour simplifier. Supposons aussi 60 électeurs, qui ne changent pas d'avis et tels que :



où 5 P L J signifie que 5 électeurs préfèrent Pierre à Louis et ce dernier est préféré à Jacques et ainsi de suite.

Organisons alors un scrutin direct : C'est PIERRE qui est élu par 23 voix sur 60 (Louis ayant 19 voix et Jacques ayant 18 voix)

Organisons un scrutin à la majorité absolue, comme le système des élections présidentielles en France : c'est LOUIS qui est élu au deuxième tour par 32 voix contre 28 voix pour Pierre

Ceci n'est pas encore satisfaisant car si nous regardons bien les préférences, on remarque que 34 personnes sur 60 préfèrent Jacques à Pierre, que 36 personnes sur 60 préfèrent Jacques à Louis (et que 32 personnes préfèrent Louis à Pierre). Donc JACQUES doit être élu car la majorité des votants le préfère aux autres candidats !

Note : si un lecteur connait l'auteur de cette étude, merci de me le faire savoir pour que je puisse lui rendre son crédit

L'imprécision des calculatrices : 

Considérons la suite définie par :

a₀ = 2

a₁ = -2 et

a_n+1 = 111 – 1130/a_n + 3000/(a_n x a_n-1)

et utilisons une calculatrice pour estimer sa limite. Il est bien possible que la calculatrice indique que cette suite tend vers 100 (ou peut-être même vers l'infini).

Pourtant, la limite de cette suite est 6.

Si un lecteur possède une calculatrice qui indique réellement cette limite, merci de m'envoyer les références de la machine ...

Dix puissance 100 (10^100), c'est-à-dire 1 suivi de cent 0 est un nombre assez petit pour les mathématiques. Ci-dessus on parle d'un nombre de près de 13 millions de chiffres. Mais en physique ce nombre est énorme et dépasse de loin tout ce qui est décemment mesurable dans l'Univers. Par exemple : l'age de l'Univers est d'environ 4x10^17 secondes, le nombre d'atomes dans l'Univers est estimé à 10^80 et le volume de l'Univers est d'environ 10^79 mètres cubes. On peut mesquiner en mesurant le volume de l'Univers avec une unité plus petite que le micromètre cube (le volume de l'Univers est de 10^97 micromètres cubes), mais ceci est-il vraiment raisonnable ?

Remarquons encore que les logiciels peuvent de nos jours factoriser des nombres de près de 100 chiffres. Par exemple : 2737882432998373449001788105858949116600231806557266964756245462889177674535386949783641407864272657

= 7822355509185635104514444159624578103641

x 3500074152578891422032544688011130305249645189353615551200377

Il y a plus de vendredi 13 que de lundi 13, mardi 13 etc ... ou si on préfère, la probabilité que le treizième jour du mois soit un vendredi est plus grande que la probabilité que ce soit un autre jour de la semaine ; n'en déplaise (ou plaise) aux amateurs (ou détracteurs) du vendredi 13.

Cette vérité ne semble pas être juste mais il y a une explication  

Il existe des nombres "forts" qui ont le même nombre de chiffres et qui gardent leurs chiffres après une multiplication.

Exemple : 1827 x 9846 = 17988642

Si un lecteur connait d'autres exemples, merci de me les envoyer ...

Les nombres parfaits sont des nombres qui sont égaux à la moitié de la somme de leurs diviseurs. Par exemple : 6 = 1/2 x (1 + 2 + 3 + 6), ou dit autrement : 6 = 1 + 2 + 3.

Depuis l'Antiquité on sait, grâce à Euclide (IIIe siècle av. J.-C.) que si

M = 2^p - 1 est premier alors 1/2 M.(M + 1) = 2^(p-1) x (2^p - 1) est parfait.

Ceci permet de calculer les nombres parfaits pairs :

6 ; 28 ; 496 ; 8128 ; 33550336 ; 8 589 869 056 etc...

On pense qu'il n'existe pas de nombres parfaits impairs....

Il existe de nombreuses "démonstrations" qui utilisent une opération impossible, comme la division par zéro. En voici un exemple : prenons un nombre a quelconque et écrivons que a = b

donc a x a = a x b

donc a x a - b x b = a x a - b x b

donc a x a + a x b - a x b - b x b = a x b -b x b

factorisons : a x (a + b) - b x (a + b) = b x (a - b)

donc (a - b) x (a + b) = b x (a - b)

simplifions : a + b = b ce qui donne a = 0, alors que a est quelconque au départ...

La faute est la "simplification" car comme a = b c'est que a - b = 0. Bien sûr, (a + b) x 0 = b x 0 mais cela permet pas de dire que a + b = b

Un grand classique :

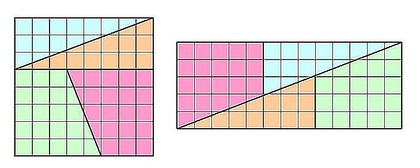
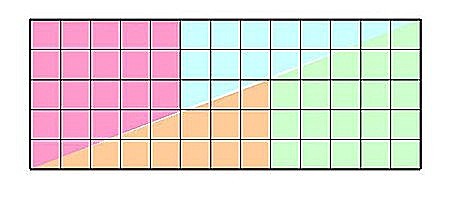
Nous dessinons un carré de 8 unités de côté. Son aire est donc de 64 unités d'aire. Puis nous découpons ce carré en 4 morceaux comme sur la figure 1 et nous recollons les 4 morceaux comme sur la figure 2

Figure 1                               Figure 2

Le rectangle a maintenant une aire de 5 x 13 = 65,

donc apparemment 64 = 65. Comment est-ce possible ?

L'explication est que la "diagonale" du rectangle a une aire de 1 unité. Si nous regardons la figure de plus près, nous remarquons que les morceaux ne s'assemblent pas rigoureusement. Il existe de nombreuses constructions similaires...

Dans une ville le barbier rase tous ceux qui ne se rasent pas eux-mêmes.

Se rase-t-il lui même ? 

Un train a autant de wagons que le nombre 0003 a de chiffres.

Le train a-t-il 4 ou 1 wagon ?

Ces énoncés sont dits indécidables.

Plus généralement, le théorème d'incomplétude, énoncé par Kurt Gödel en 1931, explique que quelle que soient les bases mathématiques, on pourra toujours trouver un énoncé qui ne peut être ni prouvé ni réfuté